알고리즘 분석
이 부록은 O’Reilly Media (2011) 에서 출간된 Allen B. Downey 의 Think Complexity 에서 발췌했습니다. Think Python 을 마치면 다음은 이 책을 고려해보세요.
알고리즘 분석(analysis of algorithms)은 알고리즘의 성능, 특히 실행 시간과 공간 요구량,을 연구하는 컴퓨터 과학의 한 분야입니다. http://en.wikipedia.org/wiki/Analysis_of_algorithms를 보세요.
알고리즘 분석의 실용적인 목표는 설계 결정을 지원하기 위해 여러 알고리즘들의 성능을 예측하는 것입니다.
2008년 미국 대통령 선거 기간에, 버락 오바마(Barack Obama) 후보는 구글(Google)을 방문했을 때 즉흥적인 분석을 요청 받은 적이 있습니다. CEO 에릭 슈밋(Eric Schmidt)은 농담 삼아 그에게 “백만 개의 32비트 정수를 정렬하는 가장 빠른 방법” 에 대해 물었습니다. 보기에 오바마가 귀띔 받은 것 같은데, 재빨리 “버블 정렬(bubble sort)은 아닐 것 같네요” 라고 대답했기 때문입니다. http://www.youtube.com/watch?v=k4RRi_ntQc8 를 보세요.
맞는 말입니다: 버블 정렬은 개념적으로는 간단하지만 커다란 데이터세트(dataset)에서는 느립니다. 아마도 슈밋이 원하던 답은 “기수 정렬(radix sort)” (http://en.wikipedia.org/wiki/Radix_sort) 일겁니다 2.
알고리즘 분석의 목표는 알고리즘들을 의미 있게 비교하는 것이지만, 몇 가지 문제가 있습니다:
- 알고리즘의 상대적인 성능은 하드웨어의 특성에 따라 다를 수 있습니다, 그래서 한 알고리즘은 기계 A 에서 더 빠르고, 다른 것은 기계 B에서 더 빠를 수 있습니다. 이 문제에 대한 일반적인 해결책은 기계 모델(machine model)을 정하고, 주어진 모델에서 알고리즘이 필요로 하는 단계나 연산의 개수를 분석하는 것입니다.
- 상대적인 성능은 데이터세트의 세부 사항에 따라 다를 수 있습니다. 예를 들어, 어떤 정렬 알고리즘들은 데이터가 이미 부분적으로 정렬되어 있을 때 더 빨리 실행됩니다. 이 문제를 회피하는데 흔히 쓰이는 방법은 최악의 사례 시나리오를 분석하는 것입니다. 때로 평균적인 사례의 성능을 분석하는 것이 유용하지만, 보통 더 어렵고, 어떤 사례 집합에 대해 평균을 취해야 하는지 분명하지 않을 수 있습니다.
- 상대적인 성능은 문제의 크기에도 영향 받습니다. 작은 리스트들에서 빠른 정렬 알고리즘이 큰 리스트들에서는 느릴 수 있습니다. 이 문제에 대해 흔히 쓰는 해결책은 실행 시간(또는 연산의 횟수)을 문제 크기의 함수로 표현하고, 함수들을 문제의 크기가 증가함에 따라 점근적으로(asymptotically) 비교하는 것입니다.
이런 종류의 비교에서 좋은 점은 알고리즘의 간단한 분류에 적합하다는 것입니다. 예를 들어, 알고리즘 A 의 실행시간이 입력의 크기, \(n\), 에 비례하고, 알고리즘 B 가 \(n^2\) 에 비례하는 경향이 있다고 알고 있다면, \(n\) 이 클 때 A 가 B 보다 빠를 거라고 기대할 수 있습니다.
이런 종류의 분석에는 주의할 점이 있지만, 나중에 다룹니다.
증가도
두 개의 알고리즘을 분석했고 그들의 실행시간을 입력의 크기로 표현했다고 가정하세요: 알고리즘 A 는 크기 \(n\) 인 문제를 푸는데 \(100n+1\) 단계가 걸립니다; 알고리즘 B 는 \(n^2 + n + 1\) 단계가 걸립니다.
다음 표는 여러 가지 문제 크기에 대해 이 알고리즘들의 실행시간을 보여줍니다:
| 입력 | 알고리즘 A의 | 알고리즘 B의 |
| 크기 | 실행 시간 | 실행 시간 |
| 10 | 1 001 | 111 |
| 100 | 10 001 | 10 101 |
| 1 000 | 100 001 | 1 001 001 |
| 10 000 | 1 000 001 | \(> 10^{10}\) |
\(n=10\) 에서, 알고리즘 A 는 아주 좋지 않습니다; 알고리즘 B 보다 거의 10배가 걸립니다. 그러나 \(n=100\) 에서 둘은 거의 비슷해지고, 더 큰 값에서는 A 가 훨씬 좋습니다.
근본적인 이유는, 큰 \(n\) 값에 대해 \(n^2\) 항을 포함한 모든 함수는, 최고 차 항(leading term)이 \(n\) 인 함수들 보다 빨리 커진다는 것입니다. 최고 차 항(leading term)은 가장 큰 지수를 갖는 항입니다.
알고리즘 A 이 경우, 최고 차 항이 큰 계수(coefficient), 100, 를 갖는데, 작은 \(n\) 에 대해 B 가 A 보다 빠른 이유입니다. 그러나 계수와 관계없이, \(a n^2 > b n\) 가 되도록 하는 \(n\) 이 항상 존재합니다.
같은 논증을 최고 차가 아닌 항들에 대해서도 적용할 수 있습니다. 알고리즘 A 의 실행시간이 \(n+1000000\) 라 할지라도, 충분히 큰 \(n\) 에서는 알고리즘 B 보다 여전히 우수합니다.
일반적으로, 더 작은 최고 차 항을 갖는 알고리즘이 큰 문제에 대해서 더 우수한 알고리즘이라고 예상합니다만 작은 문제들의 경우에는 다른 알고리즘이 더 좋아지는 분기점(crossover point)이 있을 수 있습니다. 분기점의 위치는 알고리즘의 세부사항, 입력, 하드웨어에 따라 다르기 때문에, 알고리즘 분석의 목적에서는 보통 무시됩니다. 그러나 여러분이 이 점을 잊어도 좋다는 의미는 아닙니다.
두 알고리즘이 같은 최고 차 항을 갖는다면, 어떤 게 좋은지 말하기는 어렵습니다; 다시 한번, 답은 세부사항에 따라 다릅니다. 그래서 알고리즘 분석에서는, 같은 최고 차 항을 갖는 함수들은 계수가 다르다 할지라도 동등하게 취급됩니다.
증가도(order of growth)는 점근적인 증가 양상이 동등하게 취급되는 함수들의 집합입니다. 예를 들어, \(2n\), \(100n\), \(n+1\) 은 같은 증가도에 속하는데, 대문자 O 표기법(Big-Oh notation) 으로는 \(O(n)\) 라고 쓰고, 집합의 모든 함수들이 \(n\) 에 대해 선형으로 증가하기 때문에, 종종 선형(linear)이라고 부릅니다.
최고 차 항 \(n^2\) 을 갖는 모든 함수들은 \(O(n^2)\) 에 속합니다; 이차(quadratic)라고 부르는데, 최고 차 항 \(n^2\) 을 갖는 함수들에 붙이는 단어입니다.
다음 표는 알고리즘 분석에서 가장 자주 등장하는 몇 가지 증가도들을 점점 나빠지는 순으로 보여줍니다.
| 증가도 | 이름 |
|---|---|
| \(O(1)\) | 상수(constant) |
| \(O(\log_b n)\) | 로그(logarithmic) (\(b\) 에 관계 없이) |
| \(O(n)\) | 선형(linear) |
| \(O(n \log_b n)\) | 앤로그앤(“en log en”) |
| \(O(n^2)\) | 이차(quadratic) |
| \(O(n^3)\) | 삼차(cubic) |
| \(O(c^n)\) | 지수(exponential) (\(c\) 에 관계 없이) |
로그 항의 경우 로그의 밑은 중요하지 않습니다; 밑을 바꾸는 것은 상수를 곱하는 것과 같은데, 증가도를 바꾸지는 않습니다. 비슷하게, 모든 지수 함수는 지수의 밑과 관계없이 같은 증가도에 속합니다. 지수 함수는 매우 빠르게 증가하기 때문에, 지수 알고리즘은 작은 문제에만 유용합니다.
[연습 B.1.]
대문자 O 표기법에 관한 위키피디아 페이지를 http://en.wikipedia.org/wiki/Big_O_notation 에서 읽고 다음 질문에 답하세요:
- \(n^3 + n^2\) 의 증가도는 무엇입니까? \(1000000 n^3 + n^2\) 는? \(n^3 + 1000000 n^2\) 는?
- \((n^2 + n) \cdot (n + 1)\) 의 증가도는 무엇입니까? 곱하기 전에, 최고 차 항만 필요하다는 것을 기억하세요.
- 만약 \(f\) 가 \(O(g)\), 지정되지 않은 어떤 함수 \(g\) 에 대해, 면, \(af+b\) 에 대해서는 뭐라고 말할 수 있을까요?
- 만약 \(f_1\) 과 \(f_2\) 가 \(O(g)\) 에 속하면, \(f_1 + f_2\) 에 대해서는 뭐라 말할 수 있을까요?
- 만약 \(f_1\) 가 \(O(g)\) 에 속하고 \(f_2\) 가 \(O(h)\) 에 속하면, \(f_1 + f_2\) 에 대해서는 뭐라 말할 수 있을까요?
- 만약 \(f_1\) 이 \(O(g)\) 에 속하고 \(f_2\) 는 \(O(h)\) 라면, \(f_1 \cdot f_2\) 에 대해서는 뭐라 말할 수 있을까요?
성능을 염려하는 프로그래머는 종종 이런 종류의 분석을 받아들이기 어려워합니다. 그들에게는 이유가 있습니다: 때로 계수와 최고 차 항이 아닌 항들이 실직적인 차이를 줍니다. 때로 하드웨어의 세부사항, 프로그래밍 언어, 입력의 특성이 큰 차이를 줍니다. 그리고 작은 문제에서 접근적 양상은 부적절합니다.
그러나 여러분들이 이런 주의점에 유의한다면, 알고리즘 분석은 유용한 도구입니다. 적어도 큰 문제들에서, “더 우수한” 알고리즘은 보통 더 우수하고, 때로 많이 우수합니다. 같은 증가도를 갖는 두 알고리즘간의 차이는 보통 상수 인수입니다만, 좋은 알고리즘과 나쁜 알고리즘간의 차이에는 한계가 없습니다!
기본적인 파이썬 연산들의 분석
대부분의 대수 연산은 상수 시간입니다; 곱셈은 보통 덧셈과 뺄셈보다 오래 걸리고, 나눗셈은 더 오래 걸립니다만, 이 실행 시간들은 피 연산자의 크기에 영향 받지 않습니다. 아주 큰 정수들은 예외입니다; 그 경우에 실행 시간은 숫자의 개수에 따라 증가합니다.
지수 참조 연산(indexing operations)—시퀀스나 딕셔너리의 요소들을 읽고 쓰는 것— 또한 자료 구조의 크기에 관계없이 상수 시간입니다.
시퀀스나 딕셔너리를 탐색하는 for 순환은 보통 선형인데, 순환의 바디에 있는 모든 연산들이 상수 시간인 이상 그렇습니다. 예를 들어, 리스트의 요소들을 더하는 것은 선형입니다:
total = 0
for x in t:
total += x
내장 함수 sum 도 같은 일을 하기 때문에 선형이지만, 더 효율적으로 구현되었기 때문에 더 빠른 경향을 보입니다; 알고리즘 분석의 용어로는 더 작은 최고차 항 계수를 가졌다고 합니다.
망갹 같은 순환을 문자열의 리스트를 “더하는”데 사용한다면, 실행시간은 이차인데, 문자열 접합이 선형이기 때문입니다.
문자열 메쏘드 join은 보통 더 빠른데, 문자열들의 총 길이에 대해 선형이기 때문입니다.
어림 감정으로, 순환의 바디가 \(O(n^a)\) 면 전체 순환은 \(O(n^{a+1})\) 입니다. 예외는 여러분이 순환이 상수 회수의 반복 후에 종료함을 보일 수 있을 때입니다. 만약 순환이 \(n\) 에 관계없이 \(k\) 번 실행된다면, 순환은 커다란 \(k\) 에서 조차 \(O(n^a)\) 에 속합니다.
\(k\) 로 곱하는 것은 증가도를 바꾸지 못할 뿐만 아니라 나누는 것도 마찬가지입니다. 그래서 만약 순환의 바디가 \(O(n^a)\) 이고 \(n/k\) 번 실행된다면, 순환은 커다란 \(k\) 에서 조차 \(O(n^{a+1})\) 에 속합니다.
상수 시간인 지수 참조와 len 를 제외하고는, 대부분의 문자열과 튜플 연산은 선형입니다. 내장 함수 min 과 max 는 선형입니다. 자르기(slice) 연산의 실행시간은 출력의 길이에 비례하지만 입력의 크기와는 관계없습니다.
모든 문자열 메쏘드들은 선형입니다만, 만약 문자열의 길이에 상수 상한이 있다면—예를 들어, 한 문자들에 대한 연산들— 상수 시간으로 볼 수 있습니다.
대부분의 리스트 메쏘드들은 선형입니다만, 몇 가지 예외가 있습니다:
- 리스트의 끝에 요소를 더하는 것은 평균적으로 상수 시간입니다; 때때로 자리가 없을 때 더 큰 장소로의 복사가 발생합니다만, \(n\) 연산의 총 시간은 \(O(n)\) 이기 때문에, 한 연산의 “할부(amortized)” 시간은 \(O(1)\) 이라고 말합니다.
- 리스트의 끝에서 요소를 지우는 것은 상수 시간입니다.
- 정렬은 \(O(n \log n)\) 입니다.
대부분의 딕셔너리 연산들과 메쏘드들은 상수 시간입니다만, 몇 가지 예외가 있습니다:
- copy의 실행 시간은 요소의 개수에 비례합니다만, 요소들의 크기와는 관계 없습니다(요소 자체가 아니라 참조만을 복사합니다).
- update 의 실행 시간은 매개 변수도 전달된 딕셔너리의 크기에 비례할 뿐 갱신되는 딕셔너리와는 관계없습니다.
- keys, values, items 는 새 리스트를 돌려주기 때문에 선형입니다; iterkeys, itervalues, iteritems 는 이터레이터(iterator)를 돌려주기 때문에 선형입니다. 그러나 이터레이터로 순환한다면, 순환은 선형이 될 것입니다. “iter” 함수들은 어느 정도 비용을 줄이지만, 참조하는 항목의 개수가 제한되지 않는 이상 증가도를 바꾸지는 못합니다.
딕셔너리의 성능은 컴퓨터 과학의 작은 기적들 중 하나입니다. [hashtable] 절 에서 어떻게 동작하는지 보게 될 것입니다.
[연습 B.2.]
정렬 알고리즘들에 대한 위키피디아 페이지를 http://en.wikipedia.org/wiki/Sorting_algorithm에서 읽고 다음 질문들에 답하세요:
- “비교 정렬(comparison sort)”이 뭔가요? 비교 정렬의 최악의 사례에 대한 증가도의 최선은 뭔가요? 모든 정렬 알고리즘에 대해, 최악의 사례에 대한 증가도의 최선은 뭔가요?
- 버블 정렬(bubble sort)이 증가도는 무엇이고, 왜 버락 오바마가 “아닐 것” 같다고 했을까요?
- 기수 정렬(radix sort)의 증가도는 뭔가요? 이 것을 사용하기 위해 필요한 사전조건들은 뭔가요?
- 안정 정렬(stable sort)는 무엇이고 왜 실전에서 중요할까요?
- (이름이 있는) 최악의 정렬 알고리즘은 뭔가요?
- C 라이브러리는 어떤 정렬 알고리즘을 사용하나요? 파이썬은 어떤 정렬 알고리즘을 사용하나요? 이 알고리즘들은 안정적(stable) 인가요? 아마 이 답들을 얻으려면 구글링을 해야 할 겁니다.
- 많은 비교 없는 정렬(non-comparison sort)들은 선형입니다. 그런데 왜 파이썬은 \(O(n \log n)\) 비교 정렬을 사용할까요?
검색 알고리즘 분석
검색은 컬렉션과 표적 항목을 받아서 표적이 컬렉션에 있는지 여부를 판단하는 알고리즘인데, 종종 표적의 지수를 돌려줍니다.
가장 간단한 검색 알고리즘은 “선형 검색(linear search)”인데, 컬렉션의 항목들을 차례대로 탐색하다가 표적을 발견하면 멈춥니다. 최악의 사례에서 컬렉션 전체를 탐색해야만 하기 때문에, 실행 시간은 선형입니다.
시퀀스의 in 연산자는 선형 검색을 사용합니다; find 와 count 같은 문자열 메쏘드들도 마찬가지 입니다.
만약 시퀀스의 요소들이 정렬되어 있다면, 이분 검색(bisection search)을 사용할 수 있는데, \(O(\log n)\) 입니다. 이분 검색은 아마도 여러분들이 (자료 구조가 아니라 진짜) 사전에서 단어를 찾을 때 사용할 알고리즘과 비슷합니다. 처음에서 시작해서 각 항목들을 순서대로 검사하는 대신, 가운데 있는 항목에서 시작해서, 찾는 단어가 앞과 뒤 중 어디에 있을지 검사합니다. 앞에 있다면, 시퀀스의 전반을 검색합니다. 그렇지 않다면 후반을 검색합니다. 두 경우 모두, 남은 항목의 수를 반으로 줄였습니다.
만약 시퀀스에 1,000,000 항목이 있다면, 단어를 찾거나 없다고 결론짓는데 20 단계가 걸립니다. 그러니 선형 검색보다 약 50,000 배 빠릅니다.
[연습 B.3.]
정렬된 리스트와 표적 값을 받아서 리스트에 있다면 그 값의 지수를 돌려주고, 그렇지 않으면 None 을 돌려주는 함수 bisection 을 작성하세요.
또는 bisect 모듈의 설명서를 읽은 후에, 사용할 수도 있습니다!
이분 검색은 선형 검색보다 많이 빠를 수 있지만, 시퀀스가 미리 정렬되어 있어야 하는데, 추가의 작업이 필요할 수 있습니다.
해시테이블(hashtable) 이라고 불리는 또 하나의 자료 구조가 있는데 더 빠르고—상수 시간으로 검색합니다— 항목들이 미리 정렬되어 있을 필요도 없습니다. 파이썬 딕셔너리는 해시테이블을 사용해서 구현되어있는데, 이 것이 in 연산자를 포함한 대부분의 딕셔너리 연산들이 상수 시간인 이유입니다.
해시테이블
[hashtable]
해시테이블이 어떻게 동작하고 왜 성능이 그렇게 좋은지 설명하기 위해, 저는 맵(map)의 간단한 구현으로 시작해서 해시테이블이 될 때까지 점차 개선합니다.
이 구현을 예시하기 위해 파이썬을 사용합니다만, 실제 상황에서 파이썬으로 이런 코드를 작성하지는 않을 것입니다; 여러분은 그냥 딕셔너리를 사용하면 됩니다! 그래서 이장의 나머지부분에서는, 딕셔너리가 존재하지 않고 여러분은 키를 값에 대응시키는 자료 구조가 필요하다고 상상해야 합니다. 여러분이 구현해야 할 연산들은:
- add(k, v):
- 키 k 를 값 v 로 대응시키는 새 항목을 더합니다. 파이썬 딕셔너리, d, 로 이 연산은 d[k] = v 라고 씌어집니다.
- get(target):
- 키 target 에 해당하는 값을 찾아서 돌려줍니다. 파이썬 딕셔너리, d,로 이 연산은 d[target] 이나 d.get(target) 으로 씌어집니다.
지금, 저는 각 키가 오직 한번만 나타난다고 가정합니다. 이 인터페이스의 가장 간단한 구현은 튜플의 리스트를 사용하는데, 각 튜플이 키-값 쌍입니다.
class LinearMap(object):
def __init__(self):
self.items = []
def add(self, k, v):
self.items.append((k, v))
def get(self, k):
for key, val in self.items:
if key == k:
return val
raise KeyError
add 는 키-값 튜플을 항목들의 리스트에 덧붙이는데, 상수 시간이 걸립니다.
get 은 리스트를 검색하는데 for 순환을 사용합니다: 만약 표적 키를 발견하면 해당 값을 돌려줍니다; 그렇지 않으면 KeyError 를 일으킵니다. 그래서 get 은 선형입니다.
대안은 키로 정렬된 리스트를 유지하는 것입니다. 그러면 get은 이분 검색을 사용할 수 있는데, \(O(\log n)\) 입니다. 그러나 리스트의 중간에 새 항목을 삽입하는 것은 선형이기 때문에, 최선의 선택은 아닙니다. add 와 get을 로그 시간에 구현할 수 있는 다른 자료 구조들 (http://en.wikipedia.org/wiki/Red-black_tree를 보세요) 이 있습니다만, 여전히 상수 시간만큼 좋지는 못합니다, 그러니 넘어갑시다.
LinearMap 을 개선하는 한가지 방법은 키-값 쌍들의 리스트를 작은 리스트들로 쪼개는 것입니다. 여기 BetterMap 이라 부르는 구현이 있는데, 100 LinearMap들의 리스트입니다. 곧 보게 되겠지만, get의 증가도는 여전히 선형입니다. 하지만 BetterMap 은 해시테이블로 가는 한 단계입니다:
class BetterMap(object):
def __init__(self, n=100):
self.maps = []
for i in range(n):
self.maps.append(LinearMap())
def find_map(self, k):
index = hash(k) % len(self.maps)
return self.maps[index]
def add(self, k, v):
m = self.find_map(k)
m.add(k, v)
def get(self, k):
m = self.find_map(k)
return m.get(k)
__init__ 는 n LinearMap 의 리스트를 만듭니다.
find_map 은 새 항목을 넣거나 검색할 맵을 정하기 위해 add 과 get 에 의해 사용됩니다.
find_map 은 내장 함수 hash 를 사용하는데, 거의 모든 파이썬 객체를 받아서 정수를 돌려줍니다. 이 구현의 제약은 해싱가능한(hashable) 키만 사용될 수 있다는 것입니다. 리스트나 딕셔너리와 같은 수정 가능한 형들을 해싱 가능하지 않습니다.
같다고 여겨지는 해싱 가능한 객체는 같은 해시 값을 돌려줍니다만, 역은 성립하지 않습니다: 두 개의 서로 다른 객체가 같은 해시 값을 돌려줄 수 있습니다.
find_map 은 나머지 연산자로 해시 값을 0 에서 len(self.maps) 사이의 값으로 바꿔, 결과가 리스트의 올바를 지수가 되도록 합니다. 물론, 이 것은 여러 다른 해시 값들이 같은 지수로 변환된다는 뜻입니다. 그러나 만약 해시 함수가 값들을 골고루 퍼뜨린다면 (해시 함수의 설계 기준입니다) LinearMap 당 \(n/100\) 개의 항목을 기대할 수 있습니다.
LinearMap.get 의 실행 시간은 항목의 수에 비례하기 때문에, BetterMap 가 LinearMap 보다 100 배쯤 빠를 것으로 기대합니다. 증가도는 여전히 선영입니다만, 최고 차 항의 계수가 더 작습니다. 좋습니다만, 아직 해시테이블만큼은 아닙니다.
여기 (마침내) 해시테이블을 빠르게 만드는 결정적인 아이디어가 있습니다: 만약 LinearMaps 의 최대 길이를 제한할 수 있다면, LinearMap.get 는 상수 시간입니다. 여러분이 해야 할 것은 항목들의 개수를 추적하고, LinearMap 당 항목의 수가 한도를 넘으면, 더 많은 LinearMap 들을 더해서 해시테이블의 크기를 재조정하는 것이 전부입니다.
여기 해시테이블의 구현이 있습니다:
class HashMap(object):
def __init__(self):
self.maps = BetterMap(2)
self.num = 0
def get(self, k):
return self.maps.get(k)
def add(self, k, v):
if self.num == len(self.maps.maps):
self.resize()
self.maps.add(k, v)
self.num += 1
def resize(self):
new_maps = BetterMap(self.num * 2)
for m in self.maps.maps:
for k, v in m.items:
new_maps.add(k, v)
self.maps = new_maps
각 HashMap 은 BetterMap 을 포함합니다; __init__ 는 단지 2 개의 LinearMap 으로 시작하고 항목의 수를 추적하는 num 을 초기화합니다.
get 은 단지 BetterMap 로 전달합니다. 실제적인 일은 add 에서 일어나는데, 항목의 수와 BetterMap 의 크기를 검사합니다: 같으면, LinearMap 당 항목 수의 평균이 1 이라는 뜻이라서 resize 를 호출합니다.
resize 는 앞의 것 보다 두 배 큰 새 BetterMap 을 만들고, 예전 맵에서 새 맵으로 항목들을 “리해싱(rehashing)” 합니다.
LinearMap 의 개수를 바꾸는 것은 find_map 의 나머지 연산자의 분모를 바꾸기 때문에 리해싱이 필요합니다. 이는 같은 LinearMap 으로 대응되었던 객체들이 나뉘게 된다는 뜻입니다(이게 우리가 원한거지요, 그렇지 않습니까?).
리해싱은 선형이기 때문에, resize 는 선형입니다. 좋지 않아 보일 수 있는데, 제가 add 가 상수 시간이 될 거라고 약속했기 때문입니다. 그러나 항상 확장할 필요는 없다는 것을 기억하세요, 그래서 add 는 보통 상수 시간이고 단지 가끔 선형입니다. add 를 \(n\) 번 실행하는데 필요한 일의 양이 \(n\) 에 비례하기 때문에, 각 add의 평균 시간은 상수 시간입니다!
이 것이 어떻게 동작하는지 보려면, 빈 HashTable 로 시작해서 일련의 항목들을 더하는 것에 대해 생각해보세요. 2개의 LinearMap 으로 시작하기 때문에, 처음 두 개의 추가는 빠릅니다(확장은 필요 없습니다). 각각 한 단위의 일이 필요했다고 합시다. 다음 추가는 확장이 필요하기 때문에, 처음 두 항목을 리해싱해야하고(2 단위의 일이 더 필요했다고 합시다) 세 번째 항목을 추가합니다(한 단위의 일). 다음 항목을 더하는데 1단위가 들어서, 지금까지 4 항목에 6 단위의 일이 들었습니다.
다음 add 는 5 단위가 들지만, 그 다음 세 개는 각자 1 단위만 들고, 첫 8개의 더하기에는 총 14 단위가 듭니다.
다음 add 는 9 단위가 들지만, 다음 확장 전에 7개를 더할 수 있어서, 처음 16 더하기에 총 30 단위입니다.
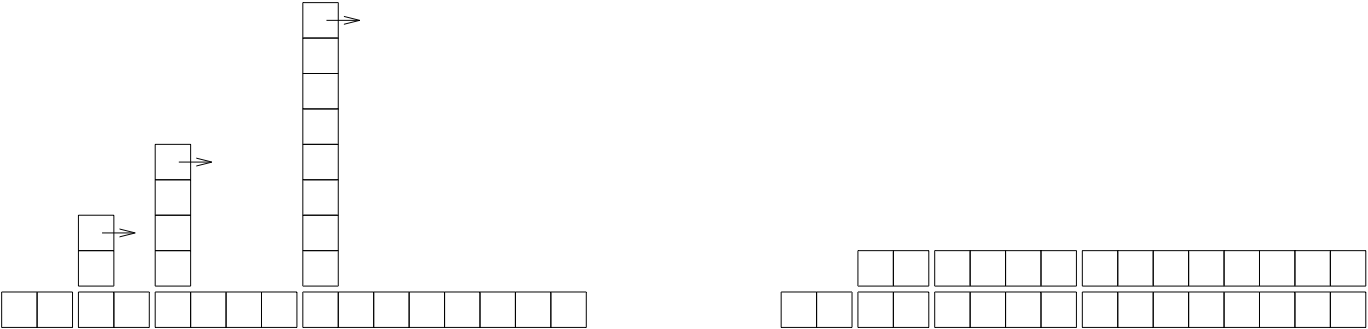
32 더하기 후에, 총 비용은 62 단위이고, 여러분이 패턴을 보기 시작했기를 바랍니다. \(n\) 더하기 후에, \(n\) 2 의 거듭제곱일 때, 총 비용이 \(2n-2\) 단위이고, 더하기 당 평균 작업은 2 단위에 조금 못 미칩니다. \(n\) 이 2 의 거듭제곱일 때가 최상의 사례입니다; \(n\) 이 다른 값일 때는 평균 작업이 조금 더 커집니다만 그리 중요하지는 않습니다. 중요한 것은 \(O(1)\) 이라는 것입니다.
그림 [fig.hash] 은 이 것들을 도식화해서 보여줍니다. 각 블럭은 한 단위의 일을 나타냅니다. 열은 각 더하기에 필요한 일의 총량을 왼쪽에서 오른쪽으로 순서대로 보여줍니다: 첫 두 adds 는 1 단위가 들고, 세 번째는 3 단위가 들고, 등등.
리해싱의 추가적인 작업은 점점 높아지면서 간격도 벌어지는 일련의 탑으로 나타납니다. 이제 탑을 넘어뜨리면, 확장의 비용을 모든 더하기에 할부해서, \(n\) 더하기 후의 총 비용이 \(2n - 2\) 임을 도식적으로 볼 수 있습니다.
이 알고리즘의 중요한 특성은 HashTable 을 확장할 때 기하급수적으로 증가한다는 것입니다; 즉 크기에 상수를 곱합니다. 만약 크기를 산술급수적으로 증가시킨다면—매번 고정된 값을 더해서— add 당 평균 시간은 선형입니다.
HashMap 의 제 구현을 http://thinkpython/code/Map.py 에서 다운로드 할 수 있습니다만, 사용해야 할 아무런 이유가 없다는 것을 기억하세요; 맵을 원한다면, 그냥 파이썬 딕셔너리를 사용하세요.